1
| renderReverse&&renderReverse({"status":0,"result":{"location":{"lng":116.33815299999995,"lat":39.94171507488761},"formatted_address":"北京市海淀区新苑街13号","business":"白石桥,车公庄,甘家口","addressComponent":{"country":"中国","country_code":0,"country_code_iso":"CHN","country_code_iso2":"CN","province":"北京市","city":"北京市","city_level":2,"district":"海淀区","town":"","adcode":"110108","street":"新苑街","street_number":"13号","direction":"附近","distance":"16"},"pois":[{"addr":"北京市海淀区三里河路1号11号楼(西苑饭店院内)","cp":" ","direction":"东南","distance":"129","name":"中国外贸金融租赁","poiType":"金融","point":{"x":116.3375433561377,"y":39.94247976148231},"tag":"金融;投资理财","tel":"","uid":"7c6d3881a8f4e35c1d5800e7","zip":"","parent_poi":{"name":"","tag":"","addr":"","point":{"x":0.0,"y":0.0},"direction":"","distance":"","uid":""}},{"addr":"三里河路5号","cp":" ","direction":"西北","distance":"105","name":"五矿发展大厦-C座","poiType":"房地产","point":{"x":116.33879200079658,"y":39.94117976632641},"tag":"房地产;写字楼","tel":"","uid":"db101a6a677f6af9c7f02567","zip":"","parent_poi":{"name":"五矿发展大厦","tag":"房地产;写字楼","addr":"北京市海淀区三里河路7号","point":{"x":116.33929505188216,"y":39.94086859358035},"direction":"西北","distance":"176","uid":"d97e2bb301449ac60b1cc703"}},{"addr":"北京市海淀区三里河路1号","cp":" ","direction":"南","distance":"225","name":"西苑饭店","poiType":"酒店","point":{"x":116.33881894996186,"y":39.943185067585059},"tag":"酒店;五星级","tel":"","uid":"eb3675036510d10201ec0197","zip":"","parent_poi":{"name":"","tag":"","addr":"","point":{"x":0.0,"y":0.0},"direction":"","distance":"","uid":""}},{"addr":"北京市海淀区三里河5号","cp":" ","direction":"西","distance":"126","name":"五矿发展大厦-B座","poiType":"房地产","point":{"x":116.33926810271686,"y":39.941553171738828},"tag":"房地产;写字楼","tel":"","uid":"a12baa40e1bdd956e956faae","zip":"","parent_poi":{"name":"五矿发展大厦","tag":"房地产;写字楼","addr":"北京市海淀区三里河路7号","point":{"x":116.33929505188216,"y":39.94086859358035},"direction":"西北","distance":"176","uid":"d97e2bb301449ac60b1cc703"}},{"addr":"北京市海淀区三里河路7号","cp":" ","direction":"西北","distance":"176","name":"五矿发展大厦","poiType":"房地产","point":{"x":116.33929505188216,"y":39.94086859358035},"tag":"房地产;写字楼","tel":"","uid":"d97e2bb301449ac60b1cc703","zip":"","parent_poi":{"name":"","tag":"","addr":"","point":{"x":0.0,"y":0.0},"direction":"","distance":"","uid":""}},{"addr":"北京市海淀区西苑饭店南门","cp":" ","direction":"东南","distance":"119","name":"新苑街-15号院","poiType":"房地产","point":{"x":116.3375164069724,"y":39.94238295419036},"tag":"房地产;住宅区","tel":"","uid":"da5b62ec876c0e3b725e8089","zip":"","parent_poi":{"name":"","tag":"","addr":"","point":{"x":0.0,"y":0.0},"direction":"","distance":"","uid":""}},{"addr":"海淀区三里河路甲1号西苑饭店副楼(动物园地铁站向西300米)","cp":" ","direction":"南","distance":"196","name":"养怡园食府","poiType":"美食","point":{"x":116.33805539027839,"y":39.943074431818278},"tag":"美食;中餐厅","tel":"","uid":"4ce10ce6608cf0b8441a321b","zip":"","parent_poi":{"name":"","tag":"","addr":"","point":{"x":0.0,"y":0.0},"direction":"","distance":"","uid":""}},{"addr":"北京市海淀区三里河路5号","cp":" ","direction":"东北","distance":"214","name":"五色土幼儿园","poiType":"教育培训","point":{"x":116.3371301356031,"y":39.940460609374458},"tag":"教育培训;幼儿园","tel":"","uid":"d6ee87244bf557e0a8f0cd7d","zip":"","parent_poi":{"name":"","tag":"","addr":"","point":{"x":0.0,"y":0.0},"direction":"","distance":"","uid":""}},{"addr":"三里河路7号","cp":" ","direction":"北","distance":"293","name":"北京国玉新疆和田玉文博馆","poiType":"购物","point":{"x":116.33848657692318,"y":39.93969995430771},"tag":"购物;商铺","tel":"","uid":"a662490a8097cd8adeee8b02","zip":"","parent_poi":{"name":"新疆大厦","tag":"酒店;其他","addr":"三里河路7号","point":{"x":116.33838776331707,"y":39.93911908469923},"direction":"北","distance":"376","uid":"50fb64fffbeb6f44e8f853ed"}},{"addr":"三里河路7号(北京西苑饭店南150米处)","cp":" ","direction":"北","distance":"314","name":"北京新疆大厦嘉宾楼","poiType":"酒店","point":{"x":116.33879200079658,"y":39.93959622795643},"tag":"酒店;其他","tel":"","uid":"dba22815e682addc4afd3ff8","zip":"","parent_poi":{"name":"新疆大厦","tag":"酒店;其他","addr":"三里河路7号","point":{"x":116.33838776331707,"y":39.93911908469923},"direction":"北","distance":"376","uid":"50fb64fffbeb6f44e8f853ed"}}],"roads":[],"poiRegions":[],"sematic_description":"中国外贸金融租赁东南129米","cityCode":131}})
|
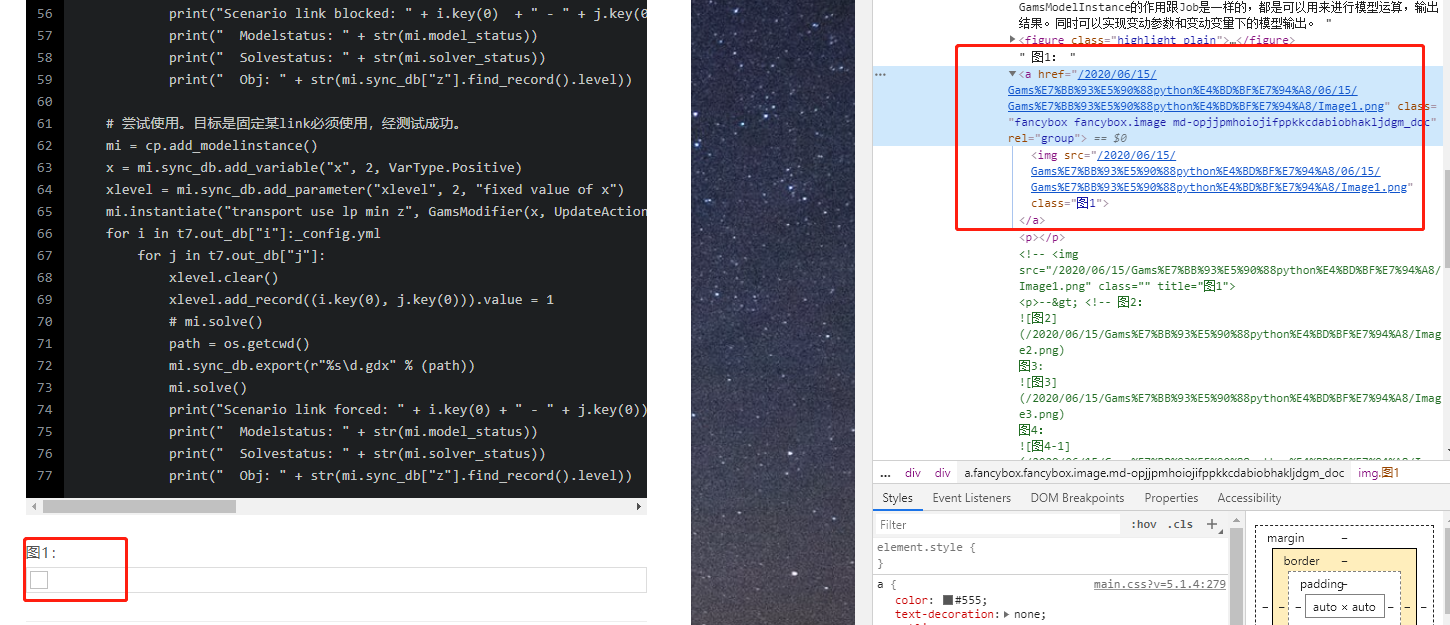 发现路径不对,图片中的可能跟你的不一样,但总而言之就是地址有问题。 3.在hexo-asset-image的github页面中的issues里发现有人提出同样的问题,然后看到说是源码的地址处理的问题。虽然开发者发现了问题,但是npm安装的依旧有问题。于是乎最简单的解决方法就是自己改index.js的源码里地址生成的部分。
发现路径不对,图片中的可能跟你的不一样,但总而言之就是地址有问题。 3.在hexo-asset-image的github页面中的issues里发现有人提出同样的问题,然后看到说是源码的地址处理的问题。虽然开发者发现了问题,但是npm安装的依旧有问题。于是乎最简单的解决方法就是自己改index.js的源码里地址生成的部分。 图2:
图2: 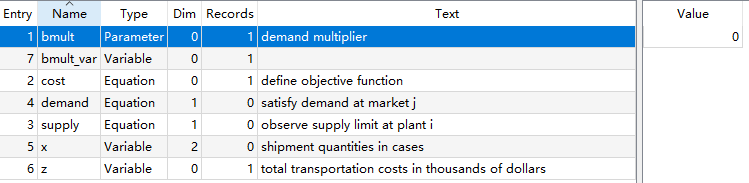 图3:
图3: 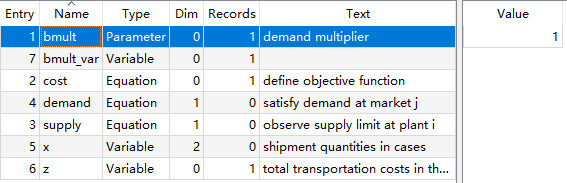 图4:
图4: 
 图5:
图5:  图6:
图6: 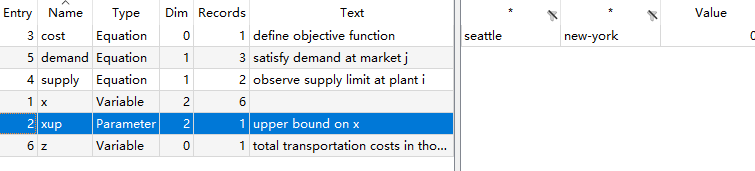
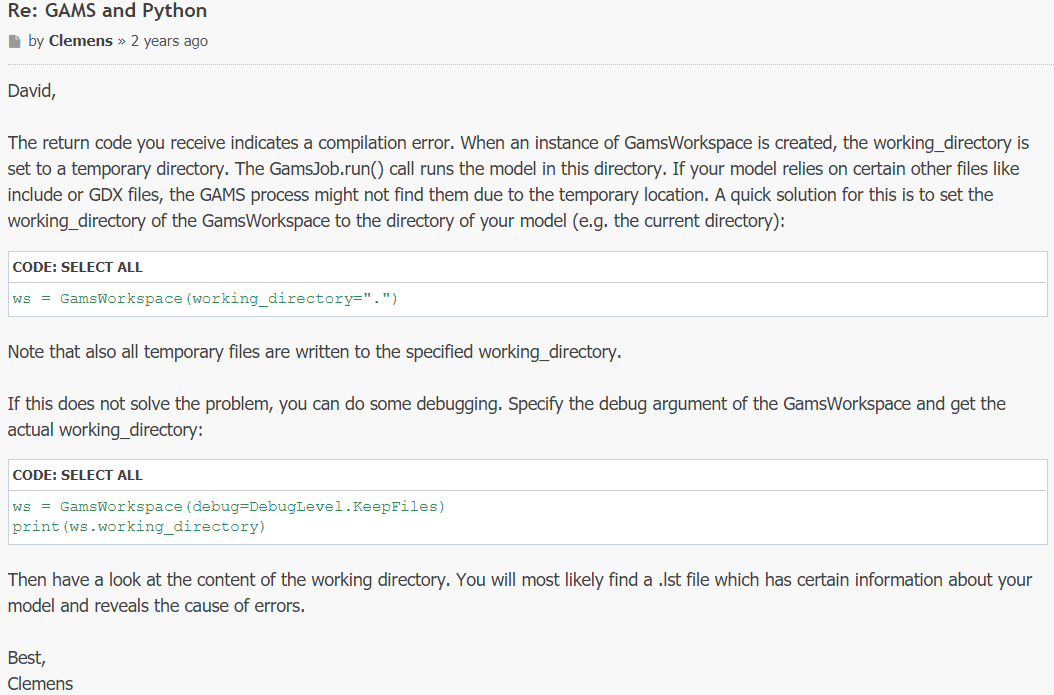 给出了详细的解释。解决方案是:
给出了详细的解释。解决方案是: 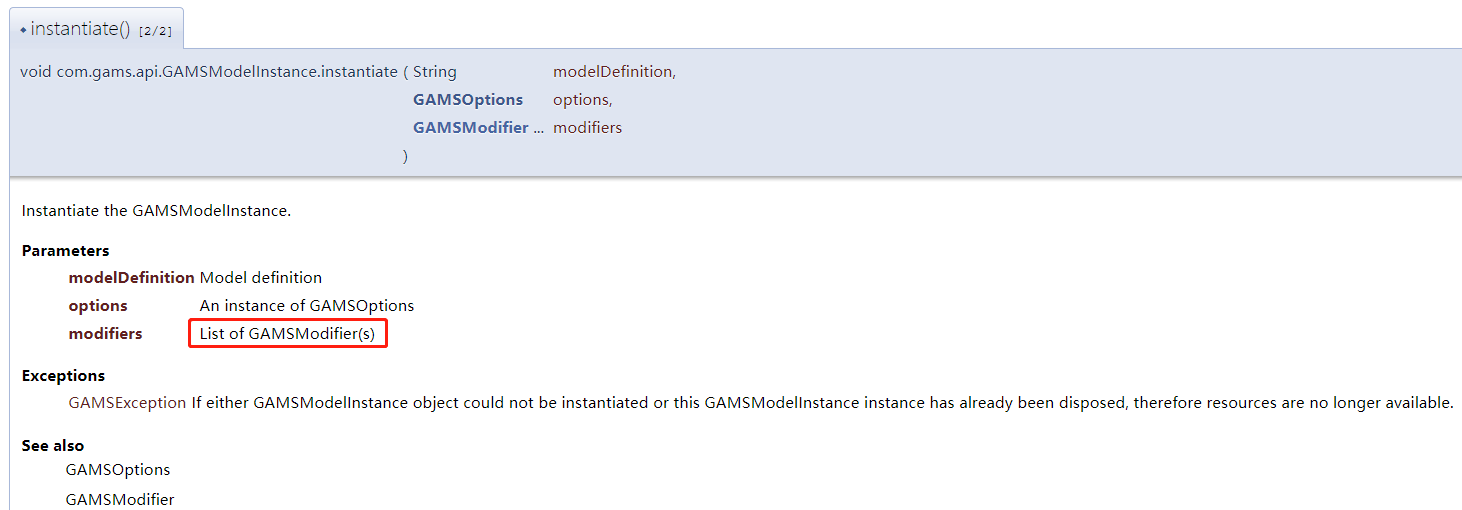
 内容如下:
内容如下: 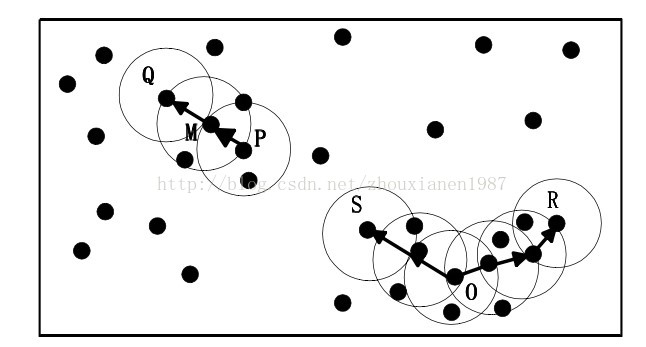 上图为“密度直达”和“密度可达”概念示意描述。根据前文基本概念的描述知道:由于有标记的各点M、P、O和R的Eps近邻均包含3个以上的点,因此它们都是核对象;M是从P“密度直达”;而Q则是从M“密度直达”;基于上述结果,Q是从P“密度可达”;但P从Q无法“密度可达”(非对称)。类似地,S和R从O是“密度可达”的;O、R和S均是“密度相连”(对称)的。 #### (3)DBSCAN密度聚类思想 DBSCAN的聚类定义很简单:由密度可达关系导出的最大密度相连的样本集合,即为我们最终聚类的一个类别,或者说一个簇。
上图为“密度直达”和“密度可达”概念示意描述。根据前文基本概念的描述知道:由于有标记的各点M、P、O和R的Eps近邻均包含3个以上的点,因此它们都是核对象;M是从P“密度直达”;而Q则是从M“密度直达”;基于上述结果,Q是从P“密度可达”;但P从Q无法“密度可达”(非对称)。类似地,S和R从O是“密度可达”的;O、R和S均是“密度相连”(对称)的。 #### (3)DBSCAN密度聚类思想 DBSCAN的聚类定义很简单:由密度可达关系导出的最大密度相连的样本集合,即为我们最终聚类的一个类别,或者说一个簇。
